holistic, structural foundation of bioregulation

\(\require{mathtools}\) See here for a relevant 12-min video introduction. This is joint work with John P Marken and Daniele Capelletti.

Biomolecular reaction networks are mathematical descriptions for the myriad processes that occur at the molecular scale to drive the behavior of cellular systems. These networks are built from two types of molecular reactions: binding and catalysis. Catalysis is reaction of the form \(A \rightarrow B\) that represent the conversion of molecules from one form to another, or equivalently the production or removal of a molecule. Binding is reaction of the form \(A + B \rightleftharpoons C\) where two molecules associate to form a complex. Inside cells, binding and catalysis reactions form interconnected networks that together determine the cells’ dynamic behavior. Therefore, to understand biological behavior amounts to understanding how binding and catalysis interact.

We claim that catalysis determines the direction of change, while binding determines how the catalysis rate is regulated. As an exmple, consider the simplest binding and catalysis network: \[ E+S \xrightleftharpoons[k_-]{k_+} C \rightarrow E+P\] where the enzyme \(E\) and substrate \(S\) binds to form complex \(C\) which is then involed in a catalysis reaction to convert to product \(P\). This system can be rewritten as the following: \[S \xrightarrow{C} P \] where we explicitly show that the net change caused by this reaction is one \(S\) molecule converted into one \(P\) molecule. This is determined by catalysis. The rate of this catalysis is proportional to the amount of complex molecules \(C\), which varies when the amount of substrates \(S\) and enzymes \(E\) varies. How \(C\) depends on \(E\) and \(S\) is determined by the binding reaction. Assuming binding reaction is fast, so achieves quasi-steady-state, we have \[C = \frac{ES}{K} \] where \(K\) is the dissociation constant of the binding reaction (other variants such as \(K_M\) can be used, depending on which part of the system is assumed fast). Also, the regulation of catalysis is in general achieved by varying the total concentrations of enzymes and substrates, which are \[t_E = E+C, \hspace{5mm} t_S = S+C.\] So how \(C\) depends on \(t_E\) and \(t_S\) characterizes the holistic regulatory profile of this catalysis reaction \(S \rightarrow P\).

(It should be noted that in special scenarios, a catalysis reaction might be regulated not by varying total concentrations, but free ones. For example, when the substrate is quorum sensing or inducer molecules that diffuse across membranes and form complexes inside the cells that cannot diffuse out. In such cases the free substrate concentration inside a cell is regulated to be in equilibrium with a large external chemical bath. However, such cases are subsets of the holistic regulatory profile, as they corresponds to having a restriction that total substrate \(t_S\) is approximately equal to free substrate \(S\). Another way to see this is that in these scenarios the external chemical bath is assumed to be held at constant concentration, i.e. have infinitely many molecules. If the external chemical bath is small, then it can no longer be considered as a control knob, but instead part of the system dynamics.)

However, beyond the simplest cases, solving for the expression of reaction complex \(C\) as a function of total reactant concentrations is analytically intractable. This is because it comes down to solving a polynomial equation of degree \(2n\) where \(n\) is the number of binding reactions, and from algebraic geometry we know there does not exist explicit solution formula for polynomials of degree higher than five. In the past, people overcome this by making assumptions, such as substrate is overabundant in Michaelis-Menten, to simplify the problem so that it is analytically solvable. This restricts to solving for regulatory profile only for special scenarios. When the problem of concern indeed satisfy the assumptions, this works extremely well. But recent advances in biology has pushed toward highly dynamic systems where such assumptions no longer hold, such as in systems in developmental biology and multi-stable biocircuits engineered in synthetic biology. So a characterization of the holistic regulatory profile is desirable.

We do this by restricting our attention to the reaction order of bioregulation. This amounts to only measure fold-change, while igonring the exact magnitude of catalysis rates. With this sacrifice, we circumvent the analytical intractability encountered when focusing on catalysis rates themselves. As a result, we can analytically characterize the holistic regulatory profile in terms of reaction order.

To intuitively understand reaction order, let us use the familiar Michaelis-Menten formula for the simple binding reaction discussed above: \[ C^{\mathrm{MM}} \approx t_E \frac{t_S}{t_S+K}. \] Plot this in log-log scale yields the following figure (blue curve).

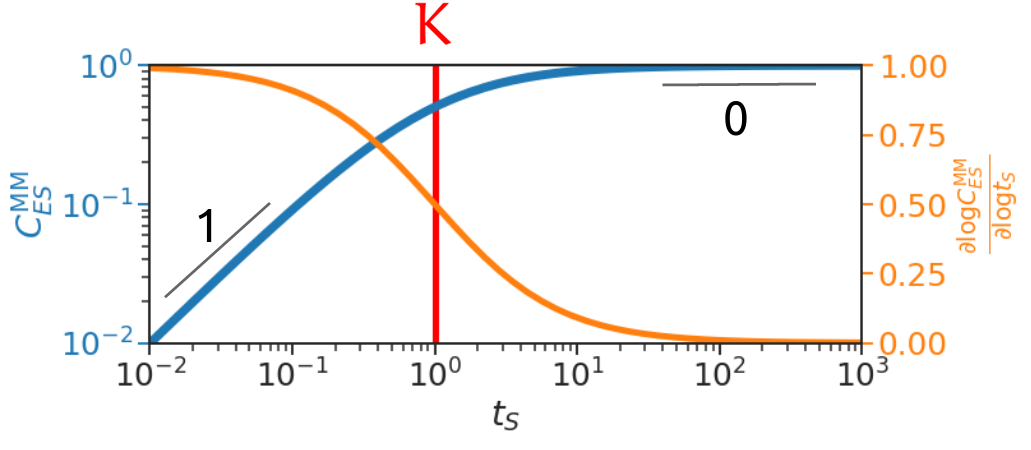
We see the slope is 1 when \(t_S\) is small, and 0 when \(t_S\) is large, and this slope is quite robust to variations in \(t_S\) at the extremes. This slope corresponds to reaction order, or the exponent of \(C\) in \(t_S\), as when slope is 1 we have \(C \approx \frac{t_E}{K} t_S\), exponent 1 in \(t_S\), and when slope is 0 we have \(C \approx t_E\), exponent 0 in \(t_S\) (independent of it). So we see reaction order captures the essence of the regulation profile, i.e. how \(C\) depends on \(t_S\) in this case. As \(t_S\) increases from low concentration, \(C\) at first linearly increases with \(t_S\), and eventually saturates out to reaction order 0.

To capture everything in between reaction order 0 and 1, we would like a continuous analogue of reaction order. We propose log derivative as this continuous analogue, which is shown as the orange curve in the above figure. We see it captures reaction orders at the extremes while smoothly varies in the middle.

Now, coming back to the goal of capturing the holistic behavior, we show that by focusing on reaction order we can analytically obtain the holistic regulatory profile. Since log derivative is a local description, we can calculate it using implicit function theorem by treating the six variables \((E,S,C,t_E,t_S,K)\) as constrained on a three-dimensional manifold. In terminology from statistical physics, we are considering a grand canonical ensemble that varies by adding or removing \((t_E,t_S)\) instead of \((E,S,C)\). This obtains the following formula: \[ \frac{\partial \log C}{\partial \log t_E, \log t_S} = \begin{bmatrix} \frac{K+S}{K+E+S} & \frac{K+E}{K+E+S} \end{bmatrix}. \] Scanning through all positive values of \(E,S,K\) characterize all possible regulatory modes the system can operate in. This results in the following figure:

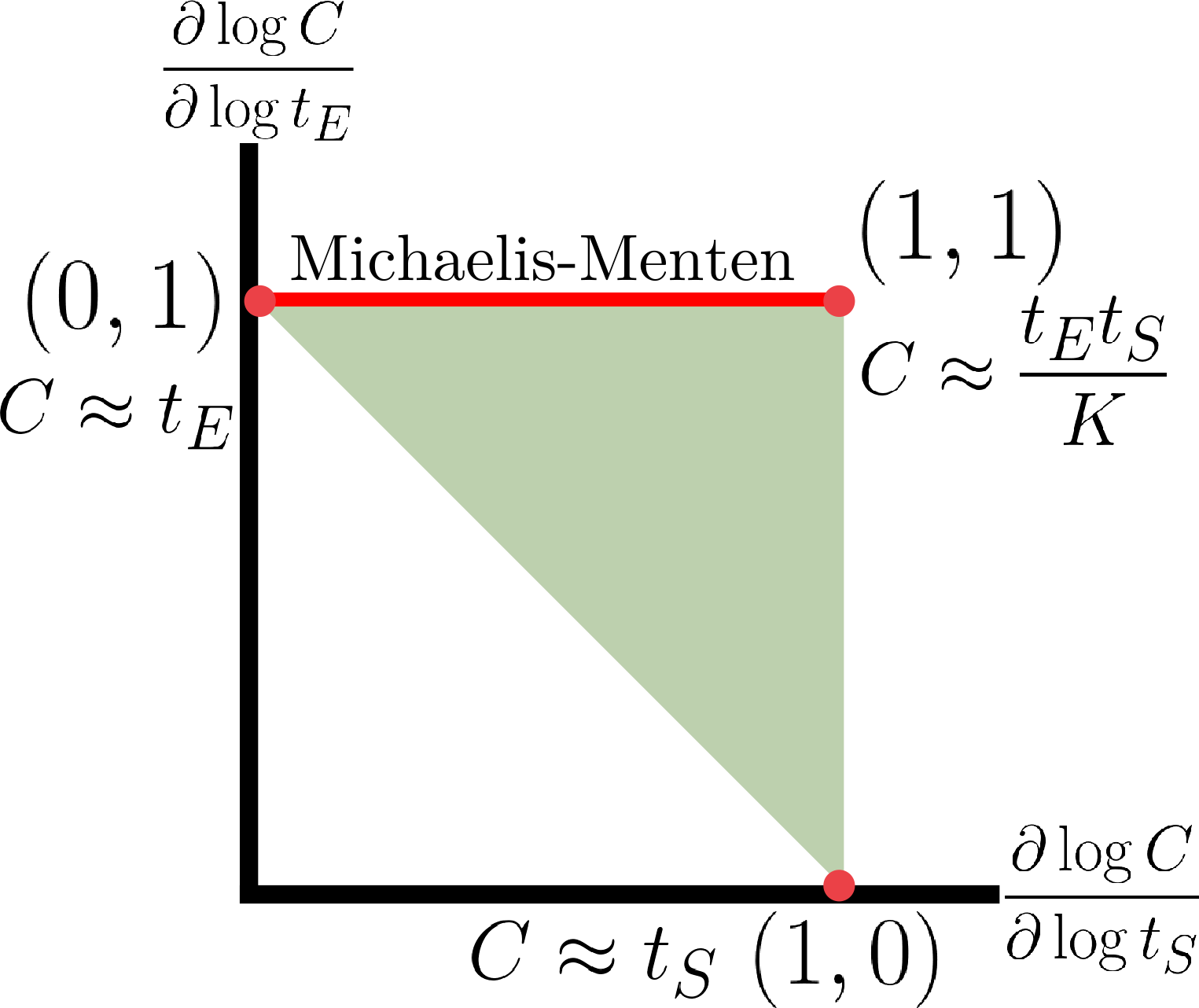
The full regulatory profile is characterzed as the triangle constraning the log derivatives. The Michaelis-Menten formula under the assumption that susbtrate is overabundant compare to enzyme corresponds to an edge of the triangle. Interestingly, this characterization naturally suggest that an approximation just as valid as the Michaelis-Menten formula is the diagonal edge between \((0,1)\) and \((1,0)\). This edge corresponds to expression \(C \approx \min \{t_E,t_S\}\). This edge is valid under condition that \(K \ll t_E,t_S\), i.e. tight binding between reactants. This condition is largely true for strong sequestrations, e.g. between sigma factors and anti-sigma factors, and in RNAi. This extreme also plays a central importance for antithetic integral control motifs proposed in this work.

For better visualization of how this triangle of log derivatives capture the holistic regulatory profile, see the following figure.

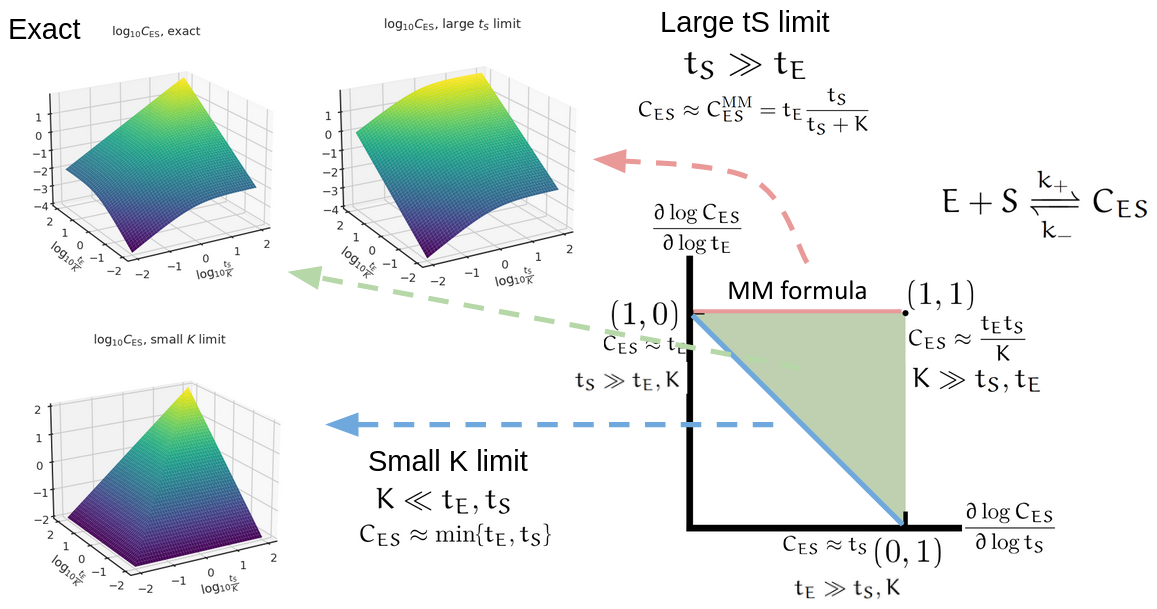
With a way to characterize the holistic regulatory profile, we can then study diverse biological problems. This could help answer the regulatory difference between an activator versus a repressor. When they work, they perform the same regulatory function. But the holistic regulatory profile can reveal how they fail in different ways. This could also be used to analyze biocircuits to find all regimes that the circuit achieves a certain function, which may reveal hidden regimes not discovered from classical Hill-function (Michaelis-Menten) based analysis. Keep tuned to our in-coming manuscript on this topic!

Another signifcant insight from this is that since catalysis is regulated by binding, and binding regulation is in terms of regulating the reaction order, this implies biological control of metabolism in cells are performed by varying the reactino order of metabolic fluxes. Formalizing this as a biological constraint enables a constraint-based approach to predict metabolism dynamics straight from network structure. See the flux exponent control page.

Apart from applications, many more work needs to be done on the mathematical foundation of log derivatives in binding networks to make this framework rigorous and easily usable. We introduce this in the mathematical foundation page. Work also needs to be done on the control theory foundation of log derivatives to see how it relates to system dynamics in general. We introduce this in the stability and control page.