Fangzhou Xiao

I’m Fang, an assistant professor in the School of Engineering at Westlake University in Xihu District, Hangzhou, CHINA, starting the biomachine architecture and control (BMAC) lab. Before this, I was a postdoctoral researcher at Suckjoon Jun group at UCSD to apply my theoretical framework in engineering to fundamental laws of bacterial survival and growth in dynamic environments. I obtained my PhD in bioengineering at Caltech in 2022, mentored by John C Doyle, and built a theoretical foundation for biocontrol in cells from gene circuits, to metabolism and physiology. My PhD thesis “Biocontrol of Biomolecular Systems: Polyhedral Constraints on Binding’s Regulation of Catalysis from Biocircuits to Metabolism” is here. Here’s my google scholar site and my CV.

My career goal is to push for the mature engineering of complex biological machines that fully realizes the unique potential of biotechnology. In order to do so, not only do we need theoretical understanding and reliable manufacturing of biological parts and components, we also need a systems theory to understand how to put parts together and what can and cannot be achieved. Examples from other engineering disciplines are Turing machines for computers, information channel for communication networks, linear input output systems for electrical circuits, and thermodynamics for heat engines.

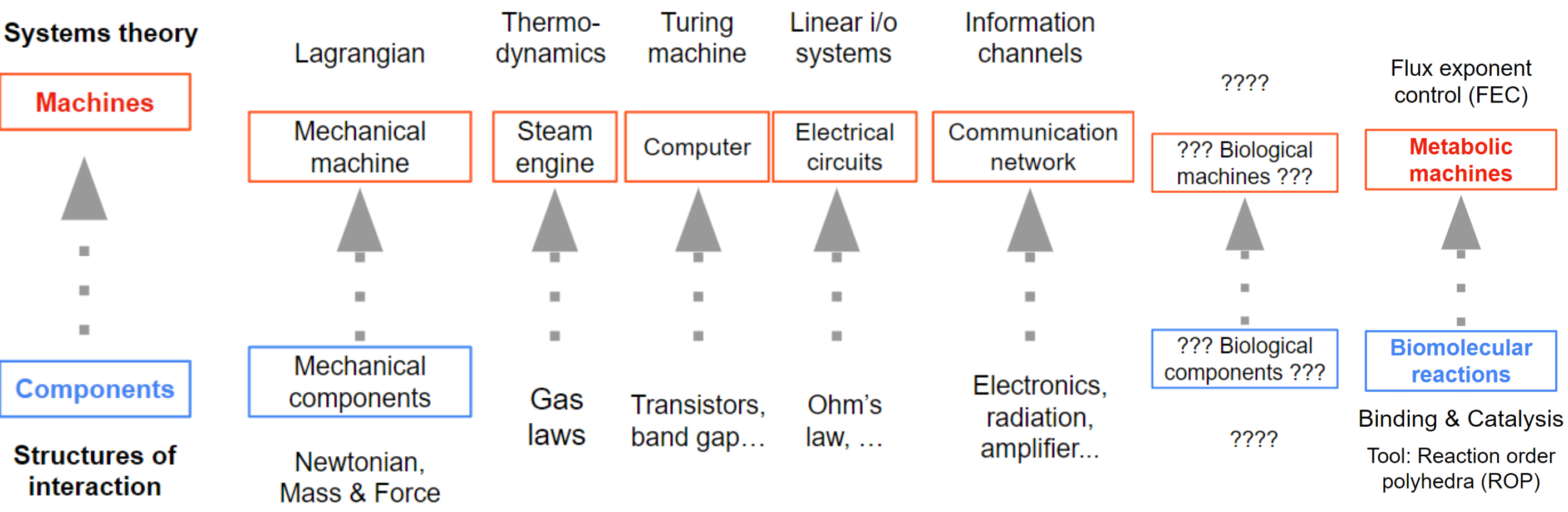
My PhD therefore focused on developing a systems theory tailored to biomolecular systems in cells. This culminated into the following statements. See the research page for details.

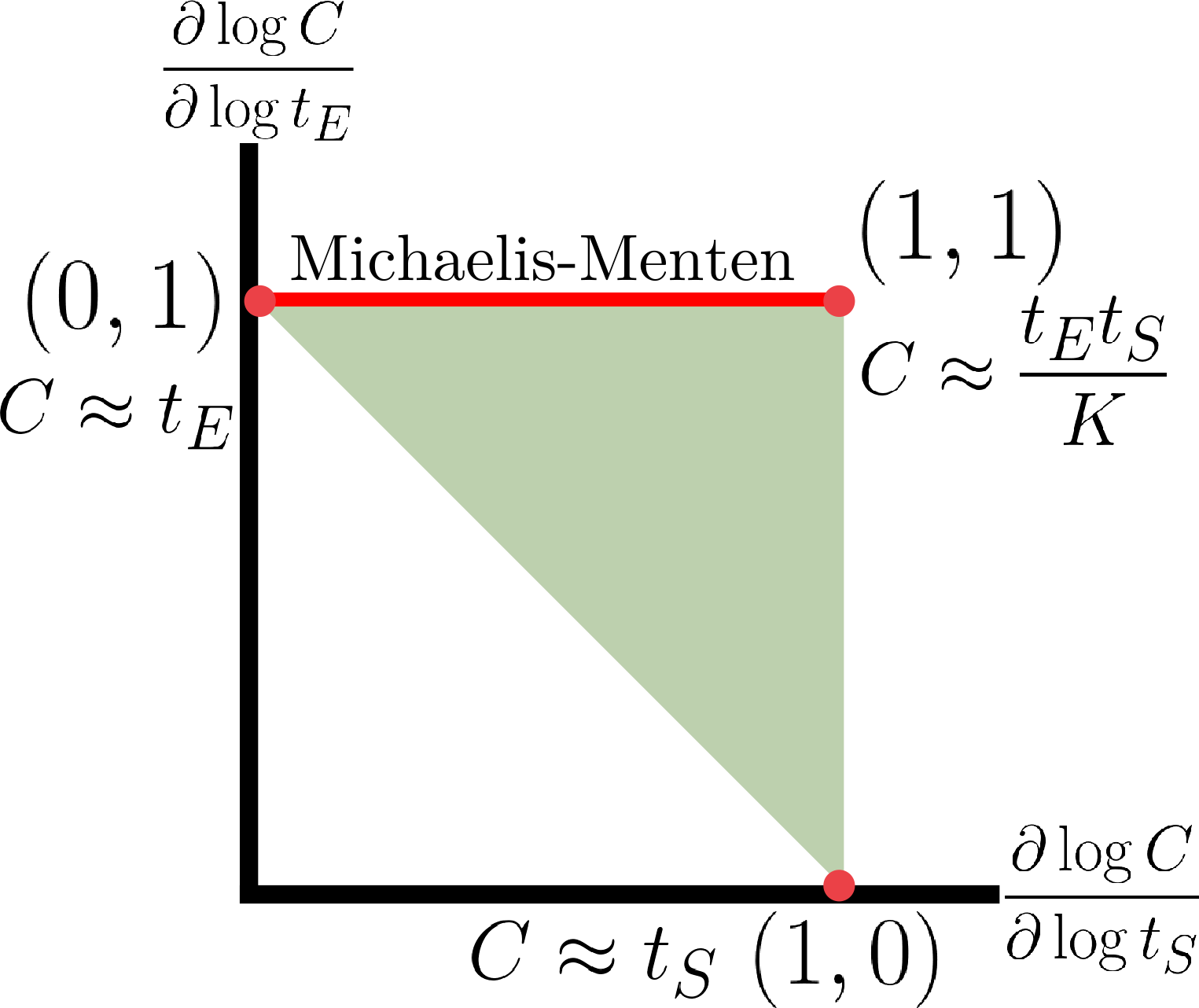
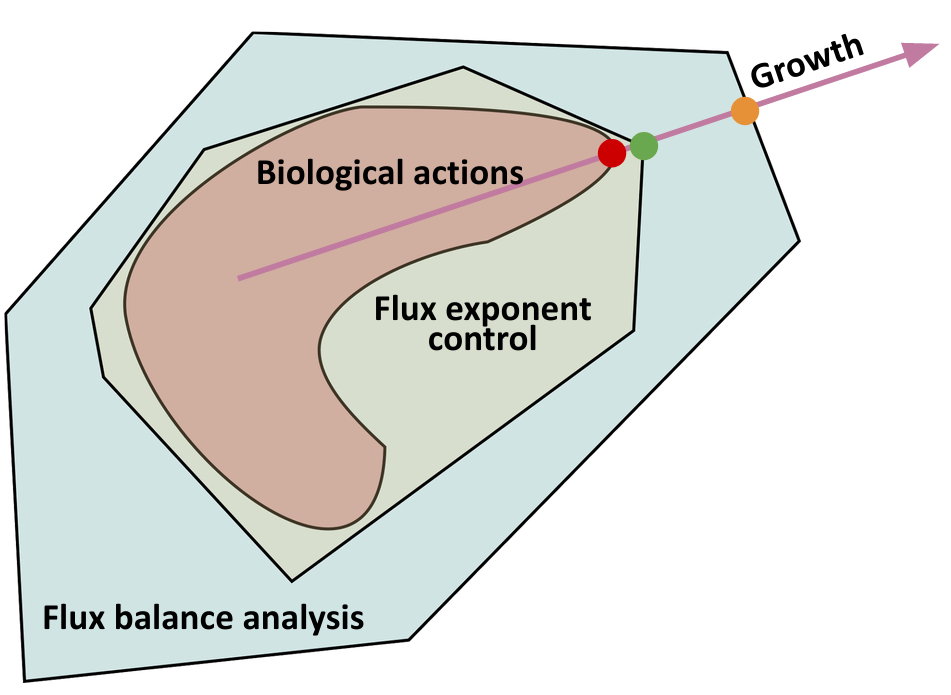
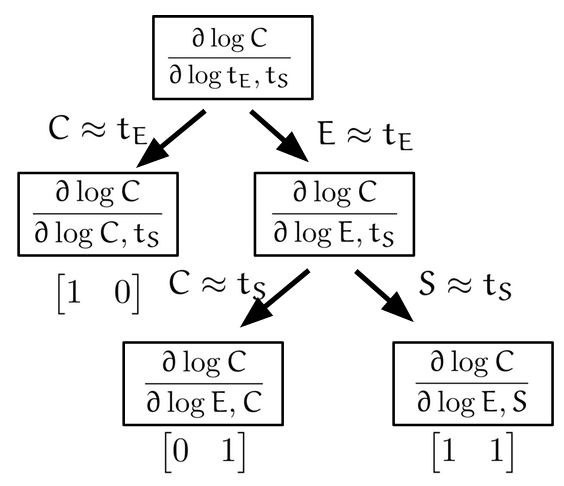
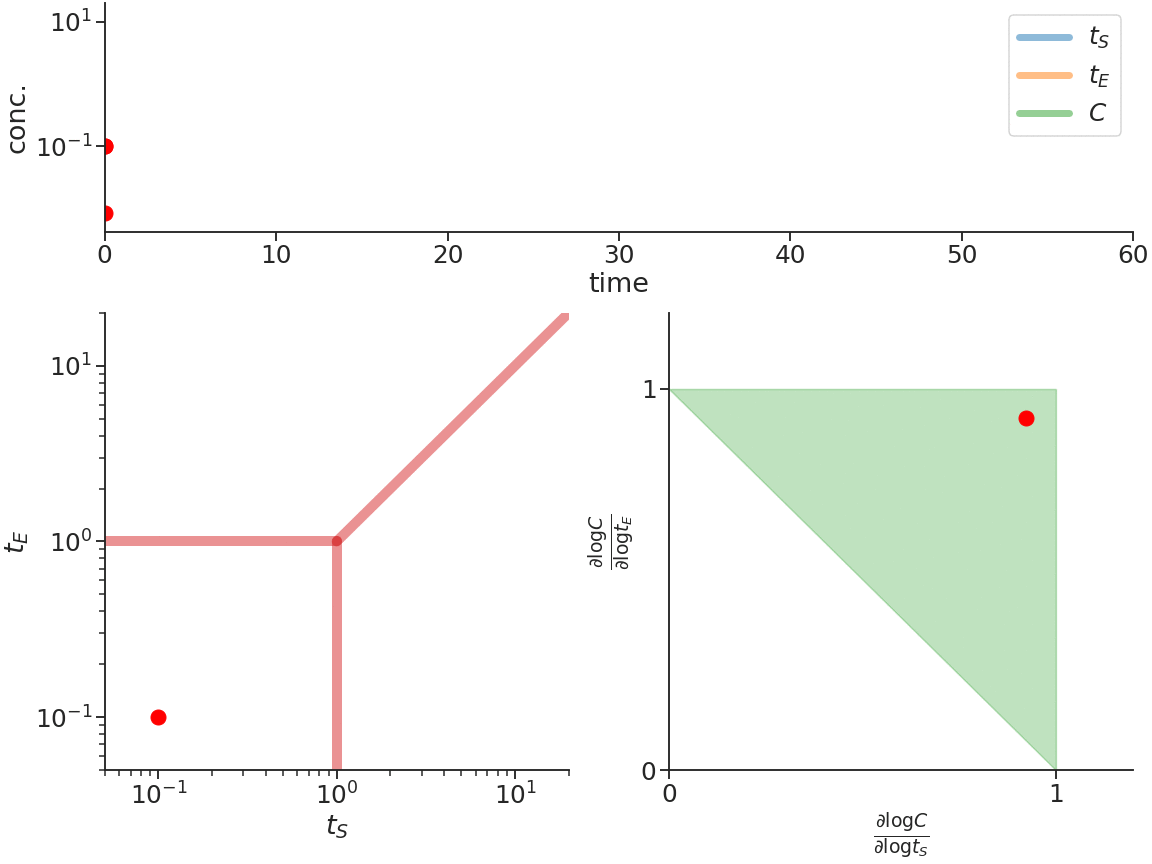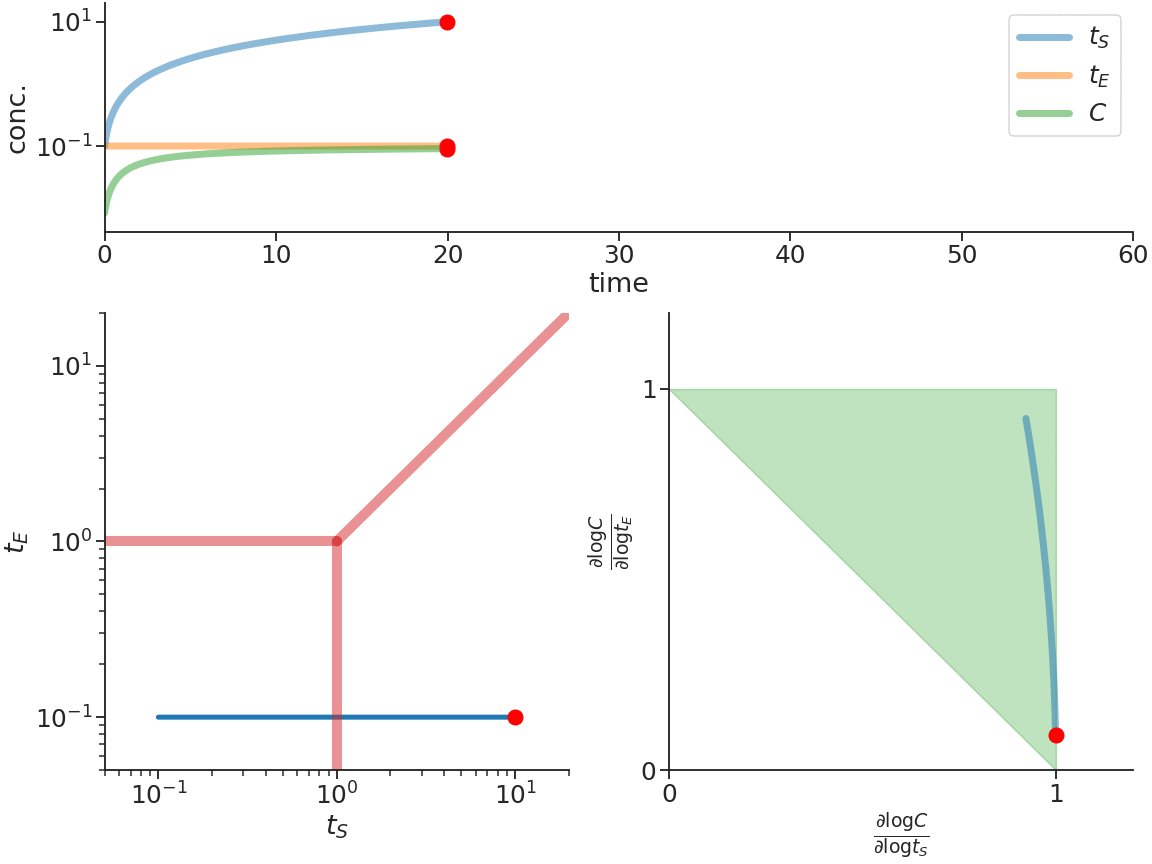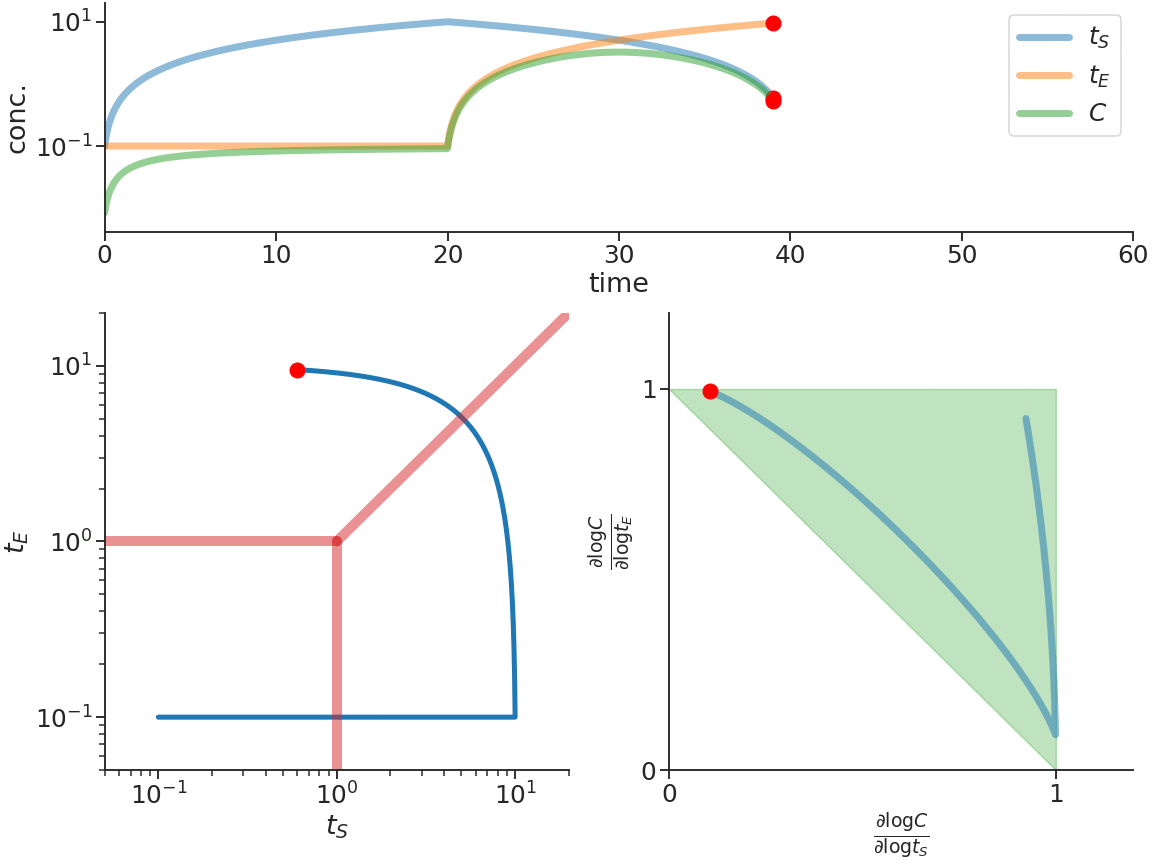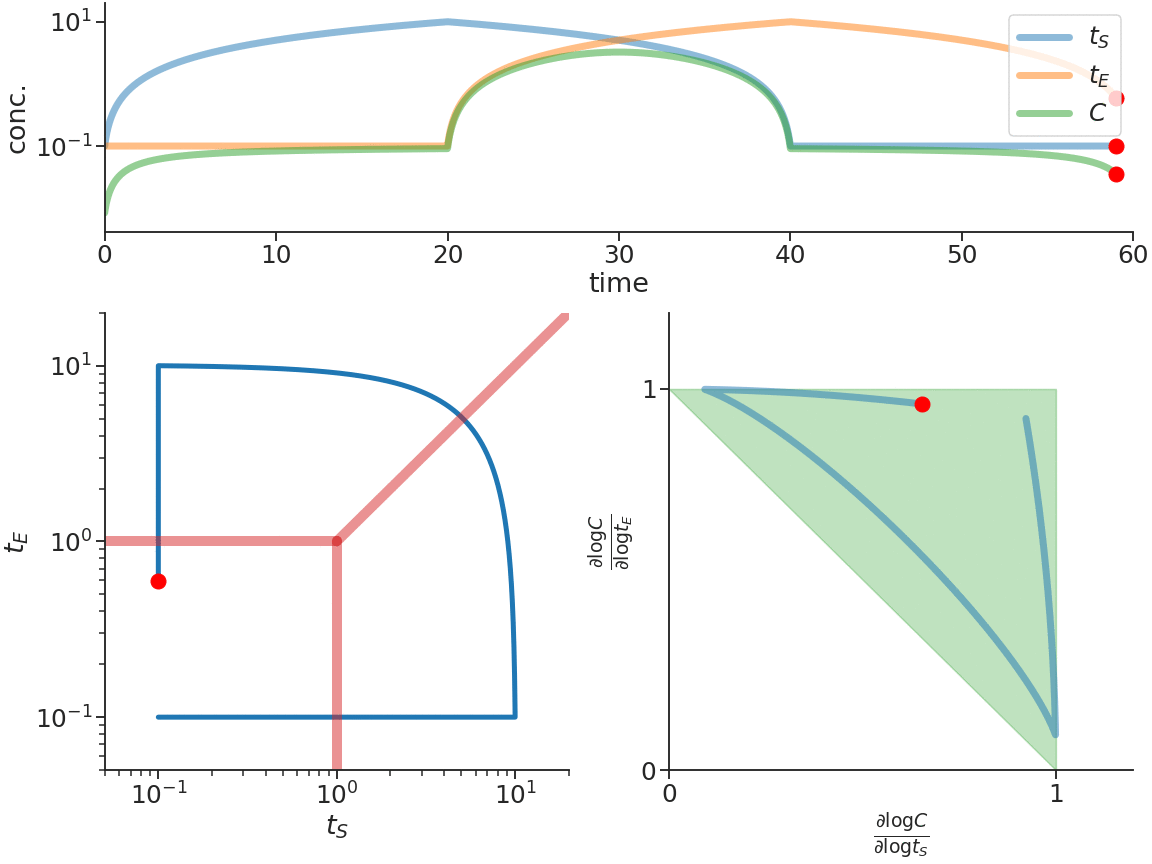
Biomolecular systems are binding and catalysis reactions. Catalysis determines the direction of change, while binding regulates how the catalysis rates vary with reactant concentrations. The holistic regulatory profile can be captured by the reaction order of catalysis, which in turn is constrained in polyhedra determined by the stoichiometry of binding. In summary, since cells control catalysis by binding, cells control catalysis rates by regulating reaction orders. This also has ramifications in several directions. On metabolism, by incorporating the constraint that reaction orders of metabolic fluxes, not the fluxes themselves, are controlled, we can predict metabolism dynamics directly from network stoichiometry, e.g. glycolytic oscillations and growth arrests. On systems biology, this derives Analysis by Binding and Catalysis (ABC) that allows discovery of necessary and sufficient conditions for a circuit to function, holistic comparisons of different circuit implementations, e.g. activator versus repressor, and enables biocircuit design where we know when a design will work, and when a design will fail. On dynamics and control of biocircuits, reaction order can work as a robust basis for stability, perfect adaptation, multistability and oscillations. Lyapunov functions and dissipativity theory tailored for biomolecular systems can be constructed based on reaction order. On the mathematics of biology, it relates bioregulation to convex polyhedra, log derivative operator decompositions, and fundamental rules of calculus for positive variables.

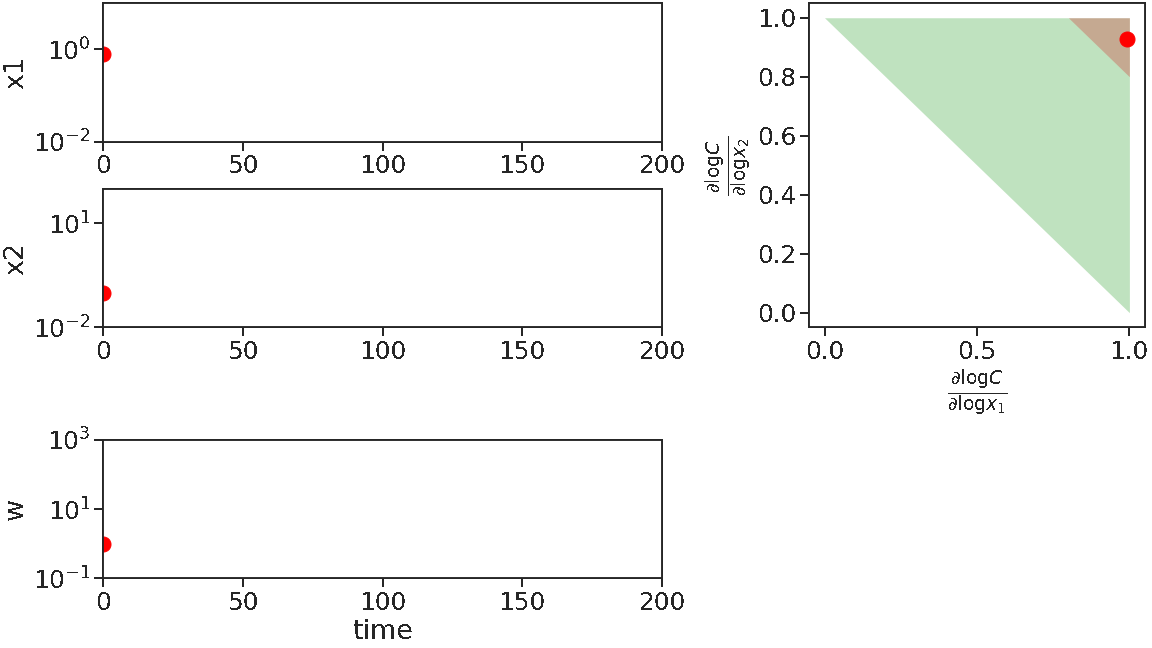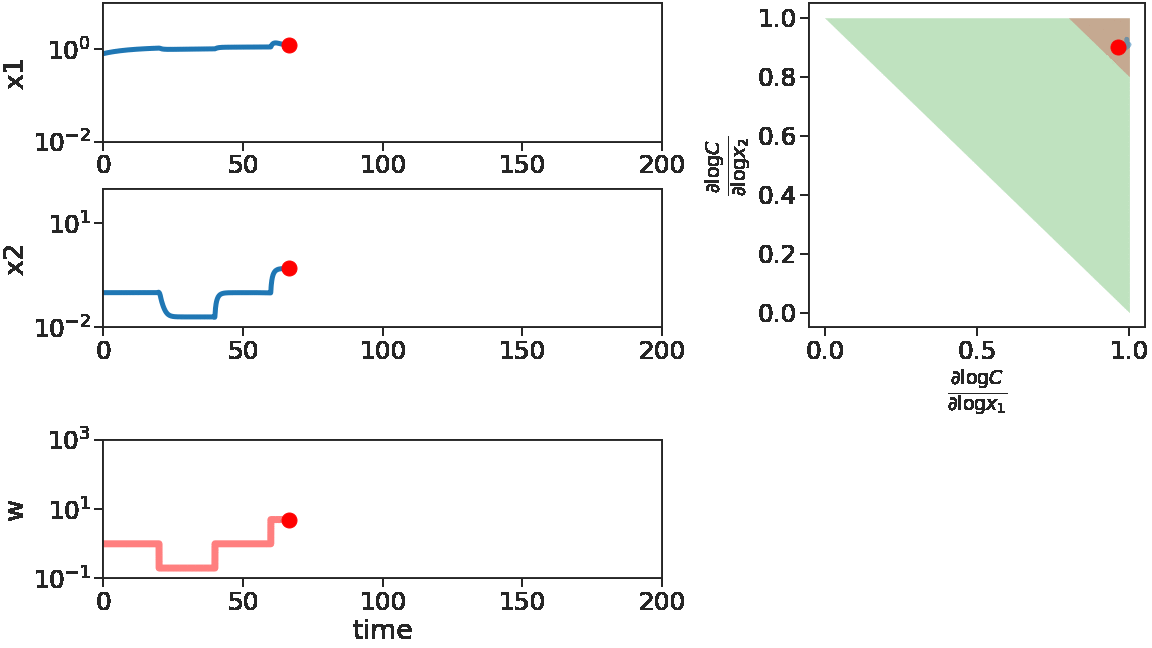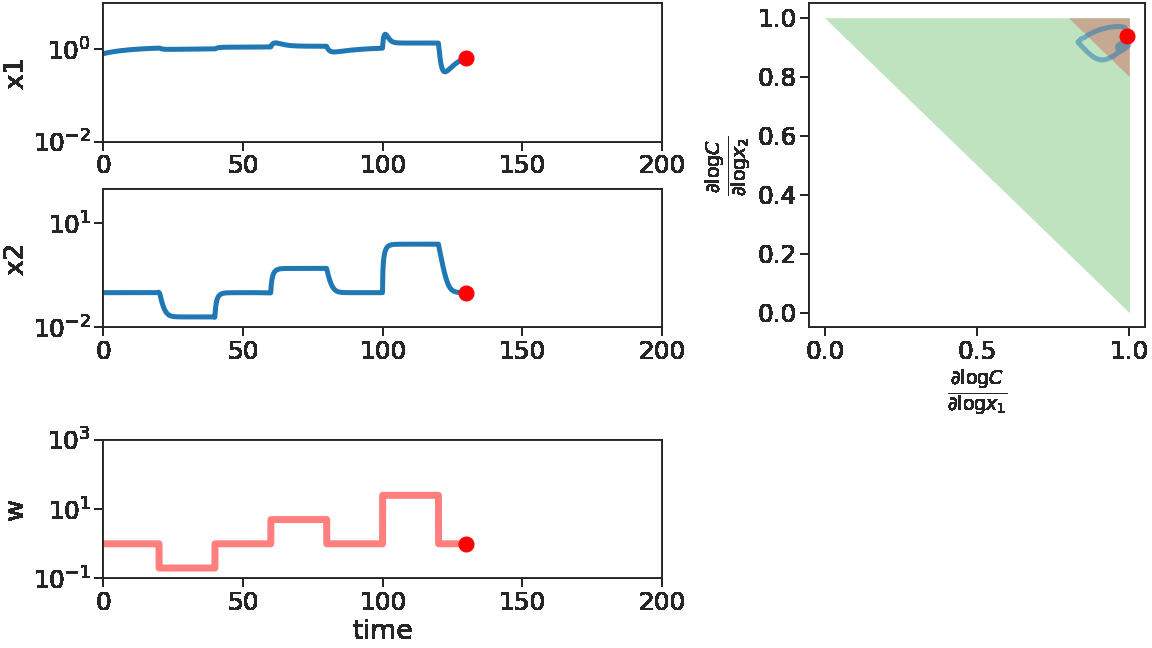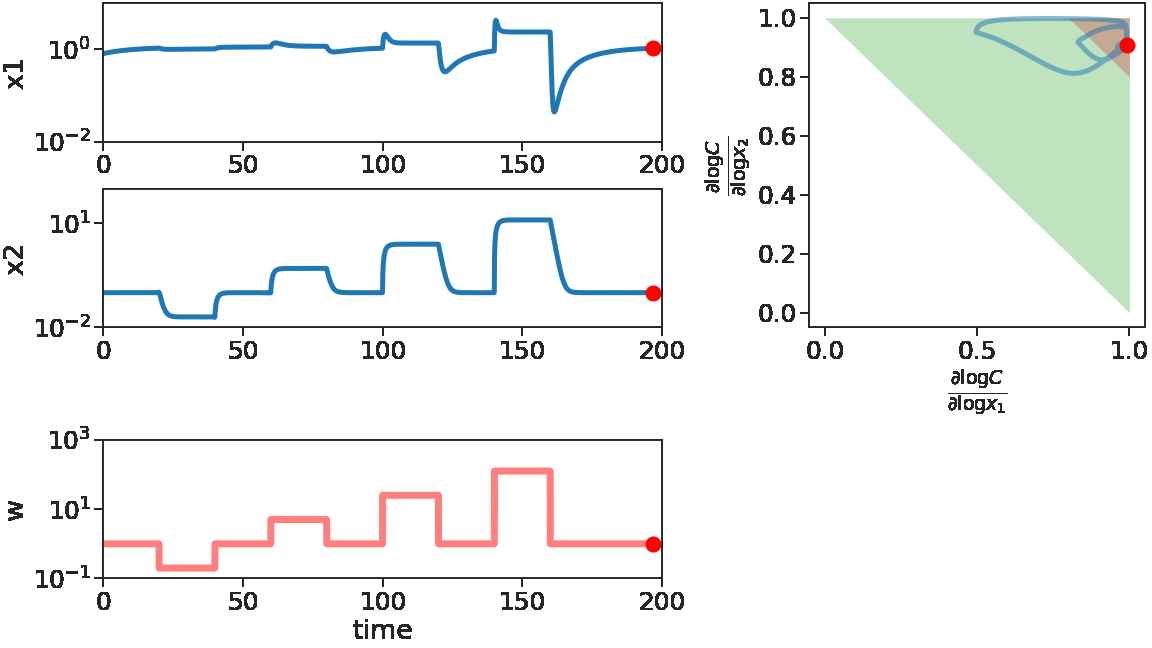
The two figures below illustrate the system view that this promotes. For more details see the research page.